ESTADISTICA DESCRIPTIVA

 Este trabajo es presentado con el fin de  desarrollar y analizar cada uno de los datos propuesto en cada ejercicio, la estadística es la ciencia que proporciona instrumentos que permiten utilizar los datos obtenidos por algún medio para la comprensión de distintos temas,

Se debe tener en cuenta que cada ejercicio es diferente, se  interpreta y  facilita la recolección de datos importantes para el estudio de situaciones, para que una investigación pueda ser realmente válida se debe tener en cuenta las técnicas de muestra, la información propicia de los datos nos permite obtener los resultados que buscamos para cualquiera que sea su utilización, medir tendencias, o empresarialmente realizar informes que permitan tomar decisiones respecto de los diferentes contextos.

    la siguiente información corresponde a las cargas máximas (en toneladas) que soportan los cables producidos en cierta fabrica:

 

9,5	9,4	9,9	10,1	10,1	10,05	10,1	10,4	10,3	10,6	10,5	10,55	10,36	10,6
10,5	10,4	10,56	10,5	10,4	10,9	10,85	11	11,03	10,9	11,1	11,15	11,1	10,95
10,8	10,9	10,85	11	11,03	10,9	11,1	11,25	11,3	11,6	11,5	11,32	11,45	11,55
11,6	11,65	11,68	11,32	11,45	11,55	11,6	11,4	11,85	11,9	12	11,95	12,1	12,15
12,3	12,4	12,65	12,9

 

CONCEPTO	VALOR
Promedio	11,08
Varianza	0,547257627
Des. Estándar	0,739768631

 

22. Se ha realizado una encuesta en 30 hogares en la que se les pregunta el número de individuos que conviven en el domicilio habitualmente. Las respuestas obtenidas han sido las siguientes:

 

4

4

1

3

5

3

2

4

1

6

2

3

4

5

5

6

2

3

3

2

2

1

8

3

5

3

4

7

2

3

 

CONCEPTO	VALOR
MEDIA	3,533333333
Varianza	3,085057471
Desv Est	1,756433167

 

3. Considerar los dos conjuntos de datos siguientes:

2	3	5	10	16	20
204	206	208	212	210	212

 

CONCEPTO	VALOR
MEDIA	208,6666667
Varianza	10,66666667
Desv Est	3,265986324

El tiempo de espera de 322 pacientes, para ser atendidos en cierto ambulatorio médico, es:

INTERVALO		FRECUENCIA	VALOR MEDIO	F. VALOR MEDIO	(V-MEDIA)^2*FREC
0	5	3	2,5	7,5	757,008555
5	10	35	7,5	262,5	4146,98386
10	15	98	12,5	1225	3394,16352
15	20	63	17,5	1102,5	49,3535647
20	25	55	22,5	1237,5	931,285203
25	30	44	27,5	1210	3655,58717
30	35	12	32,5	390	2390,76714
35	40	6	37,5	225	2192,27798
40	45	5	42,5	212,5	2907,64366
45	50	1	47,5	47,5	847,6778
		322		5920	21272,7484
MEDIA	18,3850932
VARIANZA	66,2702444
DESV ESTANDAR	8,14065381

    Se ha realizado un estudio entre 100 mujeres mayores de 15 años, observándose el número de hijos de las mismas, el resultado ha sido:

 

N. HIJOS	N. MUJERES	MEDIA
0	13	0
1	20	20
2	25	50
3	20	60
4	11	44
5	7	35
6	4	24
	100	233
MEDIA	2,33

 

 

 

 

 

   

        Dado el reporte de un almacén en el primer semestre del año para sus tres sucursales en el país.

 

	ENERO	FEBRERO	MARZO	ABRIL	MAYO	JUNIO	VENTA POR CIUDAD
CARTAGENA	3552000	2125600	2058400	3032300	4875600	5468700	21112600
MEDELLIN	2301500	2100600	1998400	2932700	3985100	4500700	17819000
BOGOTA	4750500	3400100	2985600	3002700	4923100	6130700	25192700
	10604000	7626300	7042400	8967700	13783800	16100100
MEDIA	3534666,67	2542100	2347466,67	2989233,33	4594600	5366700

 

Conclusiones:

·         El promedio de venta en la ciudad de Medellín en el primer trimestre fue de 17819000

·         En la cuidad donde se obtuvo mayor productividad de venta fue en Bogotá

 

7.  Completar la siguiente información:

El promedio geométrico sólo se aplica a números positivos y siempre resulta menor o igual que el promedio aritmético de los mismos. (la igualdad se tiene cuando todos los números promediados son iguales).

Ejemplo.

Un caso de aplicación del promedio geométrico, es el de cálculo de interés en un depósito a plazo.

 Suponga (en un caso hipotético en que las tasas no necesariamente son las que habitualmente se transan en los bancos) que una persona desea depositar $1.000.000. Durante un mes a una tasa de 2%.

Esto significa que al término del mes, el banco le entrega $1.020.000.

Al siguiente mes, toma el capital inicial más los intereses y los deposita por otro mes. Esta vez el banco ofrece una tasa de 3%. Al término del segundo mes recibe $1.050.600.

Finalmente, deposita este nuevo capital por un tercer mes, ahora al 4%, obteniendo al final $1.092.624.

¿A qué tasa mensual debería ponerse el capital inicial para obtener el mismo capital final al cabo de los tres meses?

Esta pregunta quiere dilucidar cuál sería la tasa fija que el banco debiese haber aplicado en cada uno de los tres meses en que el capital estuvo depositado (con los intereses variables - 2%, 3%, 4% - que vimos).

El capital total finalmente obtenido, puede expresarse como:

1000000*1.02*1.03*1.04 = 1000000*1.092624

Esto significa que la tasa total aplicada es de 9.2624%

Entonces, la tasa mensual estaría dada por la raíz cúbica de 1.092624, cuyo valor es 1.029968.

Es decir, se habría necesitado una tasa mensual de 2.9968%. Cantidad levemente inferior al 3% que se obtendría si, erróneamente, se hubiese promediado 2%, 3% y 4%.

Para ver claramente cómo interviene el promedio geométrico en este ejemplo, escribamos las tasas de interés como un factor multiplicativo del capital al cual se aplican. De este modo, las sucesivas tasas son: 1.02, 1.03, 1.04.

El promedio geométrico de estos números es:

 

Promedio ponderado

Tenemos 100 unidades de un producto vendidos a $1 y 1 unidad vendida a $10.
El precio promedio, según promedio simple, sería ($10 + $1) / 2 = $5,50
Pero la realidad es muy distinta.

·         100 unidades a $1 nos da $100

·         1 unidad a $10 da $10

·         En total se vendieron 101 unidades por $110.

·         El precio promedio por unidad es $110/101 = $1,089

El promedio simple de precio da $5,50.  El promedio calculado por las ventas da $1,089.  

¿Por qué esta diferencia? Porque el promedio simple, NO refleja cuando los valores a promediar (en nuestro caso, precio),tienen diferentes frecuencias (el precio $1 se repite 100 veces mientras que $10 se repite una sola vez).
Veremos en nuestro ejemplo como utilizar la función SUMA PRODUCTO de Excel para obtener el promedio ponderado

 

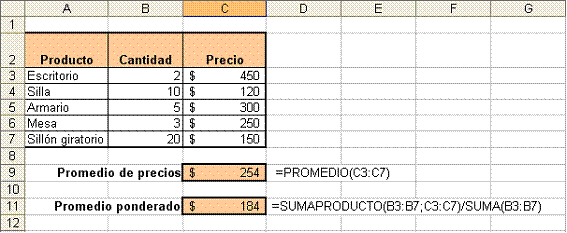
Vamos a trabajar con el ejemplo..  En la columna B tenemos un detalle de la cantidad vendida de cada producto y en la C el precio unitario. 

En la celda C9 vamos a calcular el promedio simple usando la función PROMEDIO:

=PROMEDIO (C3:C7)

El promedio “ponderado”, es decir, aquel en el cual a cada observación se le da el peso por la cantidad de veces que se repite, se calcula:

Esto es, la suma de la multiplicación (producto) de cada cantidad (frecuencia) por el precio correspondiente, lo cual se obtiene con la función SUMAPRODUCTO dividido por la suma de las cantidades.

En la celda C11, tenemos el resultado de:

=SUMA PRODUCTO (B3:B7;C3:C7)/SUMA(B3:B7)

 La media armónica (H) de un conjunto de elementos no nulos (X₁, X₂,…,X_N) es el recíproco de la suma de los recíprocos (donde 1/X_i es el recíproco de X_i)) multiplicado por el número de elementos del conjunto (N).

La media armónica es la recíproca de la media aritmética. Los elementos del conjunto deben ser necesariamente no nulos. Esta media es poco sensible a los valores grandes, pero muy sensible a los valores próximos a cero, ya que los recíprocos 1/X_i son muy altos.

La media armónica no tiene un uso muy extenso en el mundo científico. Suele utilizarse principalmente para calcular la media de velocidades, tiempos o en electrónica.

 

Ejemplo Un tren realiza un trayecto de 400km. La vía tiene en mal estado que no permitían correr. Los primeros 100 km los recorre a 120km/h, los siguientes 100km la vía está en mal estado y va a 20km/h, los terceros a 100km/h y los 100 últimos a 130km/h. Para calcular el promedio de velocidades, calculamos la media armónica.

La media armónica es de H=52,61km/h.

 

8.  El factor de crecimiento promedio de dinero compuesto con tasa de interés anual  del 10%, el 8%, el 9%, el 12% y el 7%, se obtiene determinando la media geométrica de 1.10, 1.08, 1.09, 1.12 y 1.07. Calcule el factor de crecimiento promedio.

 

x = 1.07 (7%)+ 1.08 (8%)+ 1.09 (9%)+ 1.10 (10%)+ 1.12 (12%)   = 1.09 factor promedio.

                             1.10+1.08+1.09+1.12+1.07

 

Conclusiones del 1 punto:

1.     Estos datos son no agrupados

Conclusiones del 2 punto:

2.     Estos datos no son agrupados

Conclusiones del 3 punto:

b) Qué medida utilizaría para comparar la dispersión que hay en ambos conjuntos?

R/ MEDIDA DE AMPLITUD (llamada también rango o recorrido)

c) en que conjunto hay una mayor dispersión?

R/ conjunto B= 20-2=18

Conjunto D=212-204=8

 

9 .los siguientes datos corresponden a los salarios de 10 empleados (en miles de pesos) de dos empresas de alimentos. Calcular la media, varianza, desviación estándar, y desviación media, los coeficientes de variación y de desviación media y realizar análisis comparativo. 

 

EMPRESA A: $460 $800 $710 $740 $740 $740 $750 $780 $740 $770

EMPRESA B: $425 $490 $520 $660 $710 $710 $740 $745 $760 $770

		A		B
		460		425
		800		490
		710		520
		740		660
		740		710
		740		710
		750		740
		780		745
		740		760
		770		770

MEDIA	723
VARIANZA	9178,89
DESV EST	95,8065
COEFI DE VAR	13,2512

 

MEDIA	653
VARIANZA	15995,6
DESV EST	126,474
COEF DE VAR	19,3681